Makalah Pengertian dan Jenis-Jenis Kriptografi

1.       Pengertian Kriptografi

Secara etimologi kata kriptografi (Cryptography) berasal dari bahasa Yunani, yaitu kryptos yang artinya yang tersembunyi dan graphein yang artinya tulisan (Prayudi, 2005). Awal mula kriptografi dipahami sebagai ilmu tentang menyembunyikan pesan (Sadikin, 2012), tetapi seiring perkembangan zaman hingga saat ini pengertian kriptografi berkembang menjadi ilmu tentang teknik matematis yang digunakan untuk menyelesaikan persoalan keamanan berupa privasi dan otentikasi (Diffie, 1976).

Kriptografi mempunyai 2 (dua) bagian yang penting, yaitu :

1. Enkripsi adalah proses dari penyandian pesan asli menjadi pesan yang tidak dapat diartikan seperti aslinya.
2. Dekripsi adalah merubah pesan yang sudah disandikan menjadi pesan aslinya. Pesan asli biasanya disebutplaintext, sedangkan pesan yang sudah disandikan disebut ciphertext.

                2.      Jenis-Jenis Kriptografi Modern          

•     Advanced Encryption Standart (AES)

AES adalah Advanced Encryption Standard. AES adalah block cipher yang akan menggantikan DES tetapi diantisipasi bahwa Triple DES tetap akan menjadi algoritma yang disetujui untuk penggunaan pemerintah USA. Pada Januari 1997 inisiatif AES diumumkan dan pada September 1997 publik diundang untuk mengajukan proposal block cipher yang cocok sebagai kandidat untuk AES. Pada tahun 1999 NIST mengumumkan lima kandidat finalis yaitu MARS, RC6, Rijndael, Serpent, dan Twofish.Algoritma AES dipilih pada Oktober 2001 dan standarnya dipublish pada November 2002. AES mendukung ukuran kunci 128 bit, 192 bit, dan 256 bit, berbeda dengan kunci 56-bit yang ditawarkan DES. Algoritma AES dihasilkan dari proses bertahun-tahun yang dipimpin NIST dengan bimbingan dan review dari komunitas internasional pakar kriptografi.Algoritma Rijndael, yang dikembangkan oleh Joan Daemen dan Vincent Rijmen, dipilih sebagai standar.

Tidak seperti DES yang berorientasi bit, Rijndael beroperasi dalam orientasi byte. Setiap putaran mengunakan kunci internal yang berbeda (disebut round key). Enciphering melibatkan operasi substitusi dan permutasi Karena AES menetapkan panjang kunci adalah 128, 192, dan 256, maka dikenal AES-128, AES-192, dan AES-256

Gambar 1. Panjang Kunci AES

                   Garis besar Algoritma Rijndael yang beroperasi pada blok  128-bit dengan kunci 128-bit         adalah sebagai berikut (di luar proses pembangkitan round key):

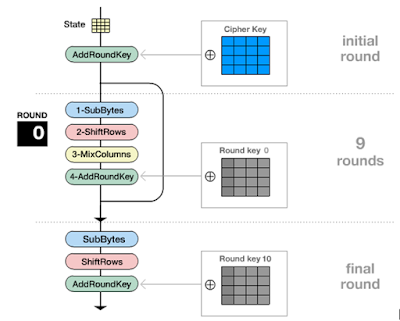
–       AddRoundKey: melakukan XOR antara state awal (plainteks) dengan cipher key.          Tahap ini disebut juga initial round.

–       Putaran sebanyak Nr – 1 kali. Proses yang dilakukan pada setiap putaran adalah:

·       SubBytes: substitusi byte dengan menggunakan tabel substitusi (S-box).

·       ShiftRows: pergeseran baris-baris array state secara wrapping.

·       MixColumns: mengacak data di masing-masing kolom array state.

·       AddRoundKey: melakukan XOR antara state sekarang round key.

–       Final round: proses untuk putaran terakhir:

·       SubBytes

·       ShiftRows

·       AddRoundKey

Algoritma Rijndael

 Selama kalkulasi plainteks menjadi cipherteks, status sekarang dari data disimpan di dalam array of bytes dua dimensi, state, yang berukuran NROWS ´ NCOLS.  Untuk blok data 128-bit, ukuran state adalah 4 ´ 4. Elemen array state diacu sebagai S[r,c], 0 £ r < 4 dan 0 £ c < Nb (Nb adalah panjang blok dibagi 32. Pada AES-128, Nb = 128/32 = 4)

Elemen Array State 

Notasi Hex

2.  Algoritma Hibrida

        Algoritma hibrida adalah algoritma yang memanfaatkan dua tingkatan kunci, yaitu kunci rahasia (simetri) – yang disebut juga session key (kunci sesi) untuk enkripsi data dan pasangan kunci rahasia – kunci publik untuk pemberian tanda tangan digital serta melindungi kunci simetri. Algoritma kriptografi yang beroperasi dalam mode bit dapat dikelompokkan menjadi dua kategori:

1)     Cipher aliran (stream cipher)

        Algoritma kriptografi beroperasi pada plainteks/cipherteks dalam bentuk bit tunggal, yang dalam hal ini rangkaian bit dienkripsikan/didekripsikan bit per bit. Stream chiper atau stream encryption merupakan suatu teknik enkripsi data dengan cara melakukan transformasi dari tiap bit secara terpisah berdasarkan posisi tiap bit dalam aliran data yang biasanya dikendalikan menggunakan operasi XOR. Enkripsi aliran data merupakan hasil dari operasi XOR antara setiap bit plaintext dengan setiap bit kuncinya. Pada stream chiper bila terjadi kesalahan selama transmisi maka kesalahan pada teks enkripsi penerima akan terjadi tepat di tempat kesalahan tersebut terjadi. Dalam praktek pertimbangan kesalahan yang mungkin terjadi sangatlah penting untuk penentuan teknik enkripsi yang akan digunakan.

       2. Cipher blok (block cipher)

        Algoritma kriptografi beroperasi pada plainteks/cipherteks dalam bentuk blok bit, yang dalam hal ini rangkaian bit dibagi menjadi blok-blok bit yang panjangnya sudah ditentukan sebelumnya.

Misalnya panjang blok adalah 64 bit, maka itu berarti algoritma enkripsi memperlakukan 8 karakter setiap kali penyandian (1 karakter = 8 bit dalam pengkodean ASCII).

Rangkaian bit

Rangkaian bit yang dipecah menjadi blok-blok bit dapat ditulis dalam sejumlah cara bergantung pada panjang blok.

Contoh: Plainteks 100111010110 dibagi menjadi blok bit yang panjangnya 4 menjadi

1001 1101 0110

Setiap blok menyatakan bilangan bulat dari 0 sampai 15, yaitu 9 13 6

Bila plainteks dibagi menjadi blok-blok yang berukuran 3 bit, maka rangkaian bit di atas menjadi:

100 111 010 110

Setiap blok menyatakan bilangan bulat dari 0 sampai 7, yaitu 4 7 2 6

Bila panjang rangkaian bit tidak habis dibagi dengan ukuran blok yang ditetapkan, maka blok yang terakhir ditambah dengan bit-bit semu yang disebut padding bits.

Misalnya rangkaian bit di atas dibagi menjadi blok 5-bit menjadi

10011 10101 00010

Blok yang terakhir telah ditambahkan 3 bit 0 di bagian awal (dicetak tebal) agar ukurannya menjadi 5 bit. Padding bits dapat mengakibatkan ukuran plainteks hasil dekripsi lebih besar daripada ukuran plainteks semula.

Cara lain untuk menyatakan rangkaian bit adalah dengan notasi heksadesimal (HEX). Rangkaian bit dibagi menjadi blok yang berukuran 4 bit dengan representasi dalam HEX adalah: 0000 = 0 0001 = 1 0010 = 2 0011 = 3

0100 = 4 0101 = 5 0011 = 6 0111 = 7

1000 = 8 1011 = 9 1010 = A 1011 = B

1100 = C 1101 = D 1101 = E 1111 = F

Misalnya, plainteks 100111010110 dibagi menjadi blok bit yang panjangnya 4 menjadi

1001 1101 0110

yang dalam notasi HEX adalah 9 D 6

Operator XOR

   Operator biner yang sering digunakan dalam cipher yang yang beroperasi dalam mode bit adalah XOR atau exclusive-or.

   Notasi matematis untuk opeartor XOR adalah ⊕ (dalam Bahas C, operator XOR dilambangkan dengan ^).

   Operator XOR diperasikan pada dua bit dengan aturan sebagai berikut:

0 ⊕ 0 = 0

0 ⊕ 1 = 1

1 ⊕ 0 = 1

1 ⊕ 1 = 0

   Operator XOR identik dengan penjumlahan modulo 2.

Misalkan a, b, dan c adalah peubah Boolean. Hukum-hukum yang terkait dengan operator XOR:

(i) a ⊕ a=0

(ii) a ⊕ b = b ⊕ a (Hukum komutatif)

(iii) a ⊕ (b ⊕ c) = (a ⊕ b) ⊕ c (Hukum asosiatif)

   Jika dua rangkaian dioperasikan dengan XOR, maka operasinya dilakukan dengan meng-XOR-kan setiap bit yang berkoresponden dari kedua ramngkaian bit tersebut.

Contoh: 10011 ⊕ 11001 = 01010

yang dalam hal ini, hasilnya diperoleh sebagai berikut:

1 0 0 1 1

1 1 0 0 1 ⊕

1 ⊕ 1 0 ⊕ 1 0 ⊕ 0 1⊕ 0 1 ⊕ 1

0 1 0 1 0

   Algoritma enkripsi sederhana yang menggunakan XOR adalah dengan meng-XOR-kan plainteks (P) dengan kunci (K) menghasilkan cipherteks:

C = P ⊕ K (6.1)

Karena meng-XOR-kan nilai yang sama dua kali menghasilkan nilai semula, maka proses dekripsi menggunakan persamaan:

P = C ⊕ K (6.2)

Contoh: plainteks 01100101 (karakter ‘e’)

kunci 00110101 ⊕ (karakter ‘5’)

cipherteks 01010000 (karakter ‘P’)

kunci 00110101 ⊕ (karakter ‘5’)

plainteks 01100101 (karakter ‘e’)

   Program komersil yang berbasis DOS atau Macintosh menggunakan algoritma XOR sederhana ini. Sayangnya, algoritma XOR sederhana tidak aman karena cipherteksnya mudah dipecahkan.

Cara memecahkannya adalah sebagai berikut (asumsi: panjang kunci adalah sejumlah kecil byte):

Ø Cari panjang kunci dengan prosedur counting coincidence sbb: XOR-kan cipherteks terhadap dirinya sendiri setelah digeser sejumlah byte, dan hitung jumlah byte yang sama. Jika pergeseran itu kelipatan dari panjang kunci (yang tidak diketahui), maka 6% dari byte akan sama. Jika tidak, maka 0.4% akan sama. Angka persentase ini disebut index of coincidence. Pergeseran terkecil mengindikasikan panjang kunci yang dicari.

Ø Geser cipherteks sejauh panjang kunci dan XOR-kan dengan dirinya sendiri. Operasi ini menghasilkan plainteks yang ter-XOR dengan plainteks yang digeser sejauh panjang kunci tersebut.Cari panjang kunci dengan prosedurcounting coincidence sbb: XOR-kan cipherteks terhadap dirinya sendiri setelah digeser sejumlah byte, dan hitung jumlah byte yang sama. Jika pergeseran itu kelipatan dari panjang kunci (yang tidak diketahui), maka 6% dari byte akan sama. Jika tidak, maka 0.4% akan sama. Angka persentase ini disebut index of coincidence. Pergeseran terkecil mengindikasikan panjang kunci yang dicari.

Ø Geser cipherteks sejauh panjang kunci dan XOR-kan dengan dirinya sendiri. Operasi ini menghasilkan plainteks yang ter-XOR dengan plainteks yang digeser sejauh panjang kunci tersebut.

Sumber :

1. http://rinas95.blogspot.co.id/2016/05/makalah-kriptografi.html

2. http://tugaskuliah-esti.blogspot.co.id/2011/10/makalah-kriptografi.html

3. https://www.academia.edu/22371107/Algoritma_Kriptografi_Modern